En las siguientes direcion se puede profundizar un poco mas sobre el tema...
Espero les sean utiles.
http://es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras
http://www.geoka.net/triangulos/teoerma_pitagoras.htmlhttp://www.sectormatematica.cl/basica/santillana/teorema_pitagoras.pdfhttp://www.rmm.cl/usuarios/cgodoy1/Flash/problem%202.swfhttp://nea.educastur.princast.es/repositorio/RECURSO_ZIP/1_jantoniozu_Fig_plan_espac/Fig_plan_espac/DOCS/problem%201.swf
domingo, 30 de octubre de 2011
sábado, 29 de octubre de 2011
ALGUNOS EJERCICIOS
Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?
Hallar el área del triángulo equilátero:
Hallar la diagonal del cuadrado:
Hallar la diagonal del rectángulo:
Hallar el perímetro y el área del trapecio rectángulo:
P = 8 + 6 + 12 + 6.32 = 32.32 cm
EJEMPLOS Y EMPLEO DEL TEOREMA...
Conociendo los lados de un triángulo, averiguar si es rectángulo
Para que un triángulo sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
Determinar si el triángulo es rectángulo.
Conociendo los dos catetos calcular la hipotenusa
Los catetos de un triángulo rectángulo miden en 3 m y 4 m respectivamente. ¿Cuánto mide la hipotenusa?
Conociendo la hipotenusa y un cateto, calcular el otro cateto
La hipotenusa de un triángulo rectángulo mide 5 m y uno de sus catetos 3 m. ¿Cuánto mide otro cateto?
¿ ESTA DEMOSTRADO?...SI LO ESTA
El Teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de Magíster matheseos.
Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.
En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.
En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
UN POCO DE HISTORIA...
El nombre asignado a este teorema se debe a que su descubrimiento recae disrectamente en la escuela pitagorica; en la antigua mesopotamia y antiguo egipto se conocian ternas con valores predeterminados que se le asignaban, a los lados de un triángulo rectángulo, y eran usados para solucionar problemas referentes a estas figuras, es lo quese registra en las antiguas tablillas y papiros.
DATO CURIOSO:
La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
DATO CURIOSO:
La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
¿QUE ES EL TEOREMA DE PITAGORAS?
En el teorema de Pitagoras podemos establecer que en todo triángulo rectángulo, el área delrectangulo de la hipotenusa ( es el lado que tiene mayor longitud en el triángulo rectángulo), es igual a la suma de las áreas del cuadrado de los catetos (son los dos lados de menor longitud del triángulo, que comforman el angulo recto)
y 
, y 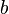la medida de la hipotenusa es 
, se establece que:
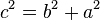
De la ecuación se deducen fácilmente 3 ejemplos de aplicación práctica:
 |  |  |
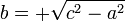Suscribirse a:
Entradas (Atom)